Generate Ethereum address from private key using plain old Python3, Elliptic Curve multiplication from SageMath and of course Keccak hash function.
import sha3
def keccak(bin):
h = sha3.keccak_256()
h.update(bin);
return h.hexdigest()
p = 2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 - 1
F = FiniteField(p)
E = EllipticCurve(F, [0, 7])
G = E([0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8])
k = 0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315
P = k * G
p = '%x' % P[0] + '%x' % P[1]
hexdigest = keccak(bytes.fromhex(p))
s_addr = hexdigest[-40:]
print('standard address: ' + '0x' + s_addr)
hexdigest = keccak(bytes(s_addr, 'UTF8'))
checksum = hexdigest[:40]
c_addr =''.join([p[0] if int(p[1], 16) < 8 else p[0].upper() for p in zip(s_addr, checksum)])
print('checksum address: ' + '0x' + c_addr)standard address: 0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9 checksum address: 0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9
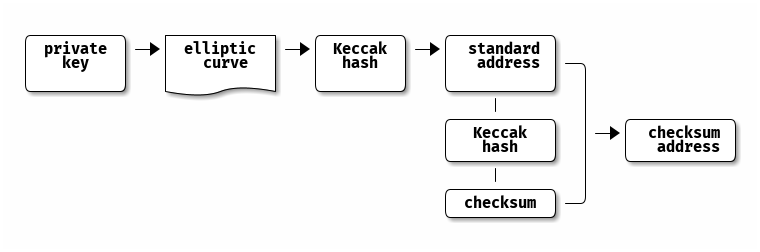
1. Hash function
Let's begin with our little helper function to calculate Keccak-256 hash:
import sha3
def keccak(bin):
h = sha3.keccak_256()
h.update(bin);
return h.hexdigest()2. Elliptic Curve
Then we have standard Secp256k1 Elliptic Curve's parameters, see generate Bitcoin address blog post for low-level implementation details.
p = 2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 - 1
F = FiniteField(p)
E = EllipticCurve(F, [0, 7])
G = E([0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8])
EElliptic Curve defined by y^2 = x^3 + 7 over Finite Field of size 115792089237316195423570985008687907853269984665640564039457584007908834671663
3. Private and public keys
Do scalar multiplication between private key k and generator G to find the public key P which is just another point on elliptic curve.
k = 0xf8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315
P = k * G
P(49790390825249384486033144355916864607616083520101638681403973749255924539515 : 59574132161899900045862086493921015780032175291755807399284007721050341297360 : 1)
4. Standard address
Address generation is done in 4 steps:
- calculate the payload which is the concatenation of hex values of each x, y coordinate of our public key
- calculate Keccak256 hash of the payload
- take last 20 bytes (40 chars)
- concatenate 0x prefix
p = '%x' % P[0] + '%x' % P[1]
print('payload: ' + p)
hexdigest = keccak(bytes.fromhex(p))
s_addr = hexdigest[-40:]
print('standard address: ' + '0x' + s_addr)payload: 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0 standard address: 0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9
5. Checksum address
Checksum address generation in 4 steps as well:
- calculate Keccak256 hash of standard address generated above (w/o the 0x prefix)
- take only first 20 bytes (40 chars)
- if the i-th nibble (character) in checksum is greater than 8 then upcase the i-th character in address, else leave unchanged, see more details in EIP-55
- concatenate 0x prefix again
hexdigest = keccak(bytes(s_addr, 'UTF8'))
checksum = hexdigest[:40]
print('checksum: ' + checksum)
print('address : ' + s_addr)
c_addr =''.join([p[0] if int(p[1], 16) < 8 else p[0].upper() for p in zip(s_addr, checksum)])
print('result : ' + c_addr)
print('checksum address: ' + '0x' + c_addr)checksum: 23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9 address : 001d3f1ef827552ae1114027bd3ecf1f086ba0f9 result : 001d3F1ef827552Ae1114027BD3ECF1f086bA0F9 checksum address: 0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9
Note
hexdigest = keccak(bytes.fromhex(p))
hexdigest = keccak(bytes(s_addr, 'UTF8'))It is imporant to understand the two lines above which might be confusing:
- the first calculates the hash of the hex value p
- the second calculates the hash of a plain text s_addr.
See the difference:
bytes.fromhex('1c')
bytes('1c', 'UTF8')b'\x1c' b'1c'