BLS signature scheme -

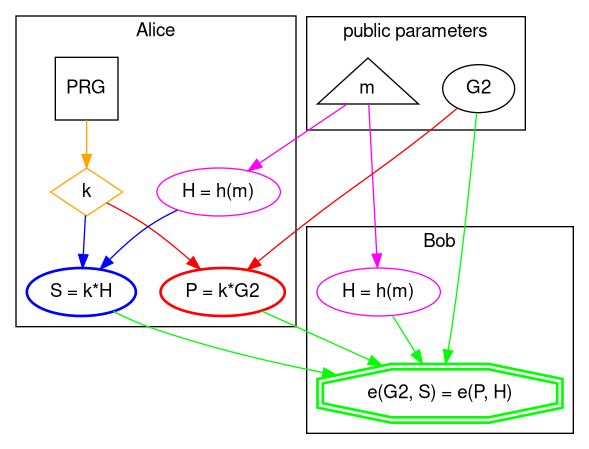
From a high level perspective this is how BLS (also known as Boneh–Lynn–Shacham) signature scheme works.

/img/bls/bls.png

  import sys
  sys.path.append("/home/icostan/Repos/pairings.py" )
  import bn256

  # helper function
  def h(msg: bytes) -> object:
      return bn256.g1_hash_to_point(msg);

  # public parameters
  m = b"Hello BLS!"
  G2 = bn256.twist_G

  # Alice
  k = bn256.rand_elem() # private key (orange)
  P = G2.scalar_mul(k)  # public key generation (red)
  H = h(m)              # hash to curve point (magenta)
  S = H.scalar_mul(k)   # signing (blue)
  # Alice sends public key 'P' and signature 'S' to Bob

  # Bob
  H = h(m)                        # hash to curve point (magenta)
  v1 = bn256.optimal_ate(G2, S)   # signature pairing
  v2 = bn256.optimal_ate(P, H)    # message pairing
  "YOU ARE A CRYPTOSTAR!" if v1 == v2 else "YOU SUCK!" # verification (green)

'YOU ARE A CRYPTOSTAR!'

Nomenclature

A bit of naming conventions first, because shapes, colors, and names have meaning:

Names

capital letter: point on elliptic curve
lower case: integer or bytes array
*: elliptic curve (scalar) multiplication
PRG: Pseudo-Random Generator

Shapes

ellipse: elliptic curve operation, points on curves
rectangle: number generator
diamond: large integer (scalar)
double octagon: pairings
triangle: bytes array

Colors

orange: private key
magenta: hash the message to elliptic curve point
red: public key generation
blue: signing
green: verification

Details

0. Library

Import BN256 elliptic curve pairing library.

  import sys
  sys.path.append("/home/icostan/Repos/pairings.py" )
  import bn256
  bn256

<module 'bn256' from '/home/icostan/Repos/pairings.py/bn256.py'>

1. Public parameters

Besides message m and generator G2 that are shown below we also know:

elliptic curves EC2 and EC1 with generator G1
target extension field TF.

but they are hidden in Barreto-Naehrig 256-bit (BN256) curve implementation.

  # helper function
  def h(msg: bytes) -> object:
      return bn256.g1_hash_to_point(msg);

  # public parameters
  m = b"Hello BLS!"
  G2 = bn256.twist_G
  type(G2)

<class 'bn256.curve_twist'>

2. Key generation

This is as simple as randomly generating private key k then multiply by generator G2 to obtain the public key, which is another point on EC2.

  # Alice
  k = bn256.rand_elem() # private key (orange)
  P = G2.scalar_mul(k)  # public key generation (red)
  type(P)

<class 'bn256.curve_twist'>

3. Signing

To sign the message m Alice has to hash the message to elliptic curve and get a point on EC1 then multiply that by private key k to obtain the signature S which is a point on EC1.

  H = h(m)              # hash to curve point (magenta)
  S = H.scalar_mul(k)   # signing (blue)
  type(S)
  # Alice sends public key 'P' and signature 'S' to Bob

<class 'bn256.curve_point'>

4. Verification

Bob receives public key P and signature S from Alice and hashes the message to curve to calculate the same H point in EC1.

Now comes the beautiful, yet so powerful part of pairing-based cryptography. Bob uses generator G2 and signature S to calculate one side of the equation, then public key P and point H to calculate the other side, if equality holds then signature is valid.

  # Bob
  H = h(m)                        # hash to curve point (magenta)
  v1 = bn256.optimal_ate(G2, S)   # signature pairing
  v2 = bn256.optimal_ate(P, H)    # message pairing
  type(v2)
  "YOU ARE A CRYPTOSTAR!" if v1 == v2 else "YOU SUCK!" # verification (green)

<class 'bn256.gfp_12'>
'YOU ARE A CRYPTOSTAR!'

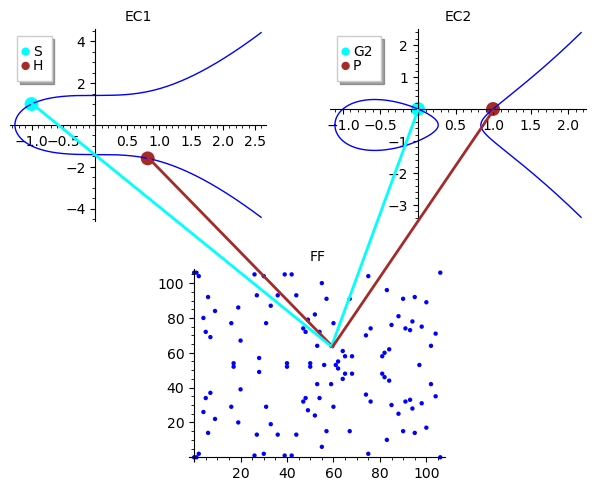
Pairing intuition

Now, the math behind pairings is quite complicated and to be honest I do not fully understand it (yet) but at least we can have a simplified visual intuition using 2 elliptic curves over rational numbers and a finite field.

/img/bls/pairings.png

You can also check the references below, lots of good resources to learn from.

Happy pairing!

References

cryptography bls pairings